Bessel Function Identities

Bessel function of the first kind of real order and complex argument. Y ν x 2 π j ν x ln x 2 γ 1 π ν 1 k 0 ν k 1. The bessel function can also be defined by the contour integral 3 where the contour encloses the origin and is traversed in a counterclockwise direction arfken 1985 p.

nonprofit degree nist standards for data destruction nist non profit degrees nist water properties non repudiation cybersecurity definition njit cybersecurity masters nonprofit management masters

Proof Of An Identity Of The Bessel Function Mathematics Stack

Solved Using The Following Representation Of The Bessel F

Bessel Function Of The First Kind From Wolfram Mathworld

Https Www Studocu Com En Us Document Colorado State University Transport Phenomena Fundamentals Lecture Notes Bessel Function Identities 1682744 View

Solved Recall The Bessel Function Of The First Kind Of Or

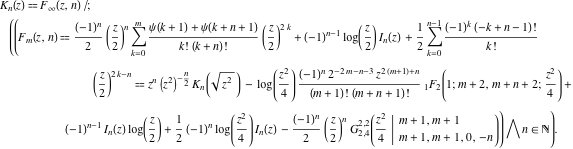
Prove Some Properties Of The Bessel Functions Of The First Kind Of

Jve v z exponentially scaled bessel function of order v.

Bessel function identities. 0 2 4 6 8 10 12 14 x 1 5 1 0 5 0 0 5 1 yn x. 1introduction to bessel functions bessel functions are the standard form of the solutions to bessel s di erential equation x2 2y x2 x y x x2 n2 y 0. 1 where nis the order of the bessel equation. Bessel functions of general order.

Bessel function also called cylinder function any of a set of mathematical functions systematically derived around 1817 by the german astronomer friedrich wilhelm bessel during an investigation of solutions of one of kepler s equations of planetary motion. If the argument is real and the order nu is integer the bessel function is real and its graph has the form of a damped vibration fig. In mathematical physics one often uses specialist books. Chapter 10 bessel functions f.

X 2 2k ν 1 π k 0 1 k 1 1 1 2 1 k 1 1 2 1 k ν k k ν. Yv v z bessel function of the second kind of real order and complex argument. For this reason the bessel functions fall under the. The bessel function of the first kind is implemented in the wolfram language as besselj nu z.

If the order is even the bessel function is even if odd it is odd. Although α and α produce the same differential equation it is conventional to define different bessel functions for these two values in. When one an alyzes the sound vibrations of a drum the partial differential wave equation pde is solved in cylindrical coordinates. It is often obtained by the separation of the wave equation 2u t2 c2r2u 2 in cylindric or spherical coordinates.

Bessel functions first defined by the mathematician daniel bernoulli and then generalized by friedrich bessel are canonical solutions y of bessel s differential equation x 2 d 2 y d x 2 x d y d x y 0 displaystyle x 2 frac d 2 y dx 2 x frac dy dx lefty 0 for an arbitrary complex number α the order of the bessel function. The bessel function of the second kind of order ν can be expressed in terms of the bessel function of the ﬁrst kind as follows. Bessel functions appear in a wide variety of physical problems. Bessel function are an inexhaustible subject there are always more useful properties than one knows.

Olver institute for physical science and technology and department of mathematics university of maryland college park maryland. X 2 2k ν bessel functions of the second kind of order 0 1 2 are shown in fig. Yn n x bessel function of the second kind of integer order and real argument.